Levenshtein distance(Basic algorithm)

By | February 14, 2026
0 Comment

The Levenshtein distance (also known as edit distance) is a metric for measuring the similarity between two strings. It’s defined as the minimum number of operations required to transform one string into the other using insertion, deletion, and substitution operations.

We can efficiently calculate the Levenshtein distance using dynamic programming.

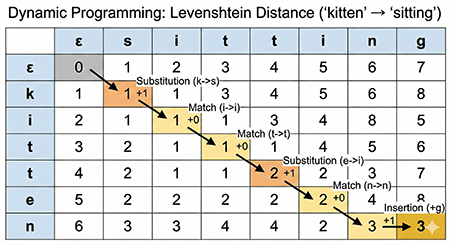
Example: Levenshtein Distance between “kitten” and “sitting”

Let’s consider two strings s1 = "kitten" and s2 = "sitting" as an example.

Here are the steps to count the number of operations:

  1. kitten → sitten (substitution: k → s)
  2. sitten → sittin (substitution: e → i)
  3. sittin → sitting (insertion: g)

In this case, the Levenshtein distance is 3.

Dynamic Programming Approach

Dynamic programming involves creating and filling in the following table:

dp[i][j] represents the Levenshtein distance between the first i characters of s1 and the first j characters of s2.

sitting
01234567
k11234567
i22123456
t33212345
t44321234
e55432234
n66543323

How to fill in the table:

  • dp[0][j] = j: The distance between an empty string and the first j characters of s2 is equal to the number of insertion operations, which is j.
  • dp[i][0] = i: The distance between the first i characters of s1 and an empty string is equal to the number of deletion operations, which is i.
  • dp[i][j] is the minimum of the following:
    • dp[i-1][j] + 1: The cost of deleting the i-th character of s1 (deletion)
    • dp[i][j-1] + 1: The cost of inserting the j-th character of s2 (insertion)
    • dp[i-1][j-1] + (0 if s1[i-1] == s2[j-1] else 1): If the i-th character of s1 and the j-th character of s2 are equal, the cost is 0; otherwise, it’s the cost of substitution (1)

Finally, dp[len(s1)][len(s2)] is the Levenshtein distance.

def levenshtein_distance(s1, s2):
    """
    Calculates the Levenshtein distance using dynamic programming.

    Args:
        s1 (str): The first string.
        s2 (str): The second string.

    Returns:
        int: The Levenshtein distance.
    """

    len_s1 = len(s1)
    len_s2 = len(s2)

    # Initialize the dp table
    dp = [[0] * (len_s2 + 1) for _ in range(len_s1 + 1)]

    # Set initial conditions
    for i in range(len_s1 + 1):
        dp[i][0] = i
    for j in range(len_s2 + 1):
        dp[0][j] = j

    # Fill in the dp table
    for i in range(1, len_s1 + 1):
        for j in range(1, len_s2 + 1):
            if s1[i - 1] == s2[j - 1]:
                cost = 0
            else:
                cost = 1

            dp[i][j] = min(
                dp[i - 1][j] + 1,  # Deletion
                dp[i][j - 1] + 1,  # Insertion
                dp[i - 1][j - 1] + cost  # Substitution
            )

    return dp[len_s1][len_s2]


# Example
s1 = "kitten"
s2 = "sitting"
distance = levenshtein_distance(s1, s2)
print(f'Levenshtein distance between "{s1}" and "{s2}": {distance}')  # Output: 3

s1 = "intention"
s2 = "execution"
distance = levenshtein_distance(s1, s2)
print(f'Levenshtein distance between "{s1}" and "{s2}": {distance}') #Output: 5

Dynamic programming allows us to efficiently calculate the Levenshtein distance. This algorithm has various applications in areas such as string similarity comparison and spell checking.

Related Posts