Calculating Fibonacci Sequence with Recursion (Basic algorithm)

By | February 14, 2026
0 Comment

What is the Fibonacci Sequence?

The Fibonacci sequence is a series of numbers where each number is the sum of the two preceding ones. It’s defined as follows:

  • F(0) = 0
  • F(1) = 1
  • F(n) = F(n-1) + F(n-2) (for n >= 2)

The sequence looks like this:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34,…

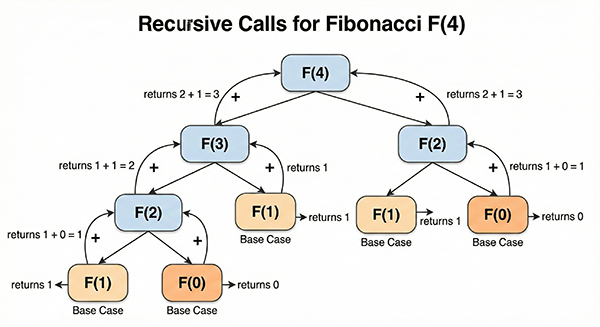
Implementing with Recursion

Recursion is a technique where a function calls itself to solve a problem. In the case of the Fibonacci sequence, you can implement it as follows:

  1. Base Cases:
    • If n is 0, return 0.
    • If n is 1, return 1.
  2. Recursive Step:
    • Otherwise, calculate F(n-1) + F(n-2) by calling the function itself.

Python Code Example

def fibonacci_recursive(n):
  """
  Calculates the nth Fibonacci number using recursion.

  Args:
    n: The desired index in the Fibonacci sequence (non-negative integer).

  Returns:
    The nth Fibonacci number.
  """
  if n == 0:
    return 0
  elif n == 1:
    return 1
  else:
    return fibonacci_recursive(n-1) + fibonacci_recursive(n-2)

# Example: Calculate the 5th Fibonacci number
result = fibonacci_recursive(5)
print(f"The 5th Fibonacci number is {result}.")  # Output: The 5th Fibonacci number is 5.

# Example: Calculate the 10th Fibonacci number
result = fibonacci_recursive(10)
print(f"The 10th Fibonacci number is {result}.") # Output: The 10th Fibonacci number is 55.

Note on Recursion

While simple and easy to understand, recursion can be inefficient. In the case of the Fibonacci sequence, the same values are calculated repeatedly, leading to exponential growth in computation time.
It becomes very slow for larger values of n.

Improvement: Memoization (Dynamic Programming)

To improve the efficiency of the recursive algorithm, you can use memoization. Memoization involves storing previously computed values and reusing them when needed instead of recalculating them.
This significantly reduces computation time.

def fibonacci_memoization(n, memo={}):
  """
  Calculates the nth Fibonacci number using memoization.

  Args:
    n: The desired index in the Fibonacci sequence (non-negative integer).
    memo: A dictionary to store calculated results (defaults to an empty dictionary).

  Returns:
    The nth Fibonacci number.
  """
  if n in memo:
    return memo[n]
  if n == 0:
    result = 0
  elif n == 1:
    result = 1
  else:
    result = fibonacci_memoization(n-1, memo) + fibonacci_memoization(n-2, memo)

  memo[n] = result # Store the calculated result
  return result

# Example: Calculate the 5th Fibonacci number
result = fibonacci_memoization(5)
print(f"The 5th Fibonacci number is {result}.")  # Output: The 5th Fibonacci number is 5.

# Example: Calculate the 10th Fibonacci number
result = fibonacci_memoization(10)
print(f"The 10th Fibonacci number is {result}.") # Output: The 10th Fibonacci number is 55.

In this memoized version, a dictionary called memo is used to store the calculated results.
Each time the function is called, it first checks if the value is already stored in memo. If it is, that value is returned. Otherwise, it calculates recursively and stores the result in memo before returning it.

  • Recursion is a technique for solving problems by breaking them down into smaller subproblems of the same type.
  • Calculating the Fibonacci sequence is a good example of recursion, but can be inefficient.
  • Optimization techniques like memoization can significantly improve the efficiency of recursive algorithms.

Related Posts