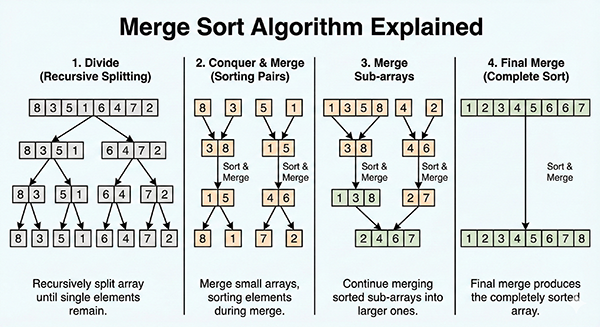
Merge Sort (basic algorithm)

By | February 14, 2026
0 Comment

Merge sort is an efficient sorting algorithm based on the divide-and-conquer paradigm. It recursively divides a large array into smaller sub-arrays, sorts those sub-arrays, and then merges them back together to create the final sorted array.

Features:

  • Stable Sort: Maintains the relative order of equal elements.
  • Time Complexity: O(n log n) in best, average, and worst cases.
  • Space Complexity: Requires O(n) additional memory (used for storing sub-arrays).

Algorithm Steps

  1. Divide: Recursively divide the array into halves until the sub-arrays have a size of 1 or 2 elements.
  2. Conquer: Consider sub-arrays with sizes of 1 or 2 to be already sorted.
  3. Merge: Merge the sorted sub-arrays to create new sorted arrays.

Example

Let’s look at the process of sorting the array [8, 3, 1, 7, 0, 10, 2] using merge sort.

  1. Divide:
    • [8, 3, 1, 7], [0, 10, 2]
    • [8, 3], [1, 7], [0, 10], [2]
    • [8], [3], [1], [7], [0], [10], [2]
  2. Conquer:
    • Each sub-array has a size of 1, so they are considered sorted.
  3. Merge:
    • [3, 8], [1, 7], [0, 10], [2]
    • [1, 3, 7, 8], [0, 2, 10]
    • [0, 1, 2, 3, 7, 8, 10]

Python Code

def merge_sort(arr):
  """
  Sorts an array using merge sort.

  Args:
    arr: The array to be sorted.

  Returns:
    A new sorted array.
  """
  if len(arr) <= 1:
    return arr  # Return the array as is if it has 1 or fewer elements

  mid = len(arr) // 2  # Calculate the middle index of the array
  left = arr[:mid]  # Left sub-array
  right = arr[mid:] # Right sub-array

  # Recursively sort the sub-arrays
  left = merge_sort(left)
  right = merge_sort(right)

  # Merge the sorted sub-arrays
  return merge(left, right)


def merge(left, right):
  """
  Merges two sorted arrays.

  Args:
    left: The sorted left array.
    right: The sorted right array.

  Returns:
    A new merged and sorted array.
  """
  result = []
  i = 0
  j = 0

  while i < len(left) and j < len(right):
    if left[i] <= right[j]:
      result.append(left[i])
      i += 1
    else:
      result.append(right[j])
      j += 1

  # Add any remaining elements from the sub-arrays
  result += left[i:]
  result += right[j:]

  return result


# Example usage
arr = [8, 3, 1, 7, 0, 10, 2]
sorted_arr = merge_sort(arr)
print(f"Before sorting: {arr}")
print(f"After sorting: {sorted_arr}")
  • Merge sort uses recursive calls, which can lead to stack overflow for very large arrays. Consider an iterative implementation in such cases.
  • Merge sort is a stable sorting algorithm, meaning it preserves the relative order of equal elements. This can be important in certain applications.

Related Posts