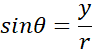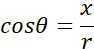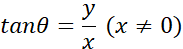
Lengths and ratios of right-angled triangles (Basic knowledge)
Trigonometric functions (sin, cos, tan, etc.) are frequently used in machine learning as tools to effectively work with angles, periods, rotations, and positions.
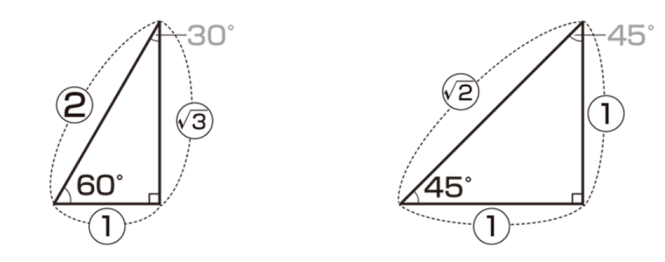
Once the angles of a right triangle are determined, the ratio is also determined. Commercially available set squares have well-known trigonometric ratios.
As shown in the figure, the ratio (trigonometric ratio) of a right triangle is determined once the angles are determined.
(sin, cos, tan) are trigonometric ratios (ratios in right-angled triangles) expressed as fractions.
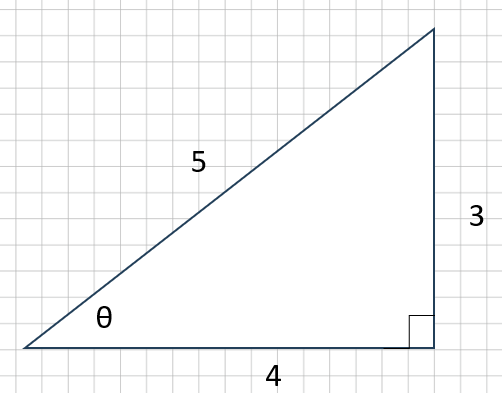
sin, cos are also a fractional representation of the ratio of the right triangle.
The length can be calculated from this trigonometric ratio.
Once you know the hypotenuse and angle, you can find the height and base.
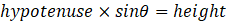
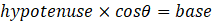
If you know the base and the angle, you can find the height and the base.
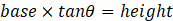
Draw the triangle and equation on a piece of paper and try to find the solution.
How to calculate sin, cos, and tan in SymPy
import sympy
# # Define the angle (30 degrees)
degree = 30
# Convert to radians (use sympy.pi to keep the value accurate)
rad = sympy.pi * degree / 180
# Calculate each value
sin_30 = sympy.sin(rad)
cos_30 = sympy.cos(rad)
tan_30 = sympy.tan(rad)
print(f"sin(30°): {sin_30}")
print(f"cos(30°): {cos_30}")
print(f"tan(30°): {tan_30}")Three basic triangles (the basis for calculations)
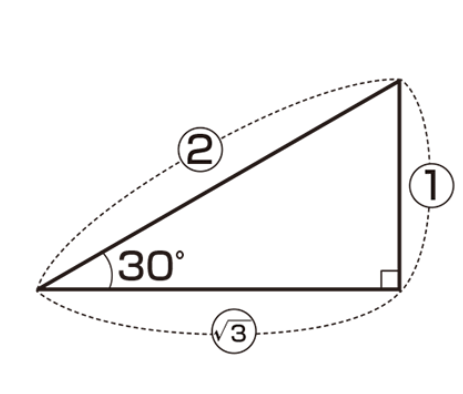
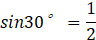
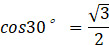
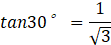
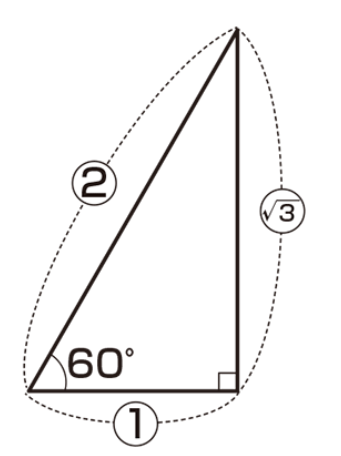
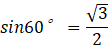
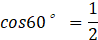
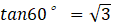
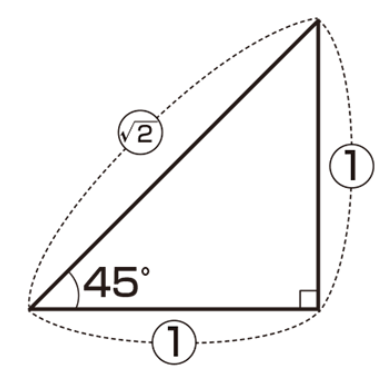
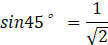
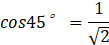
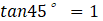
Expansion Angles
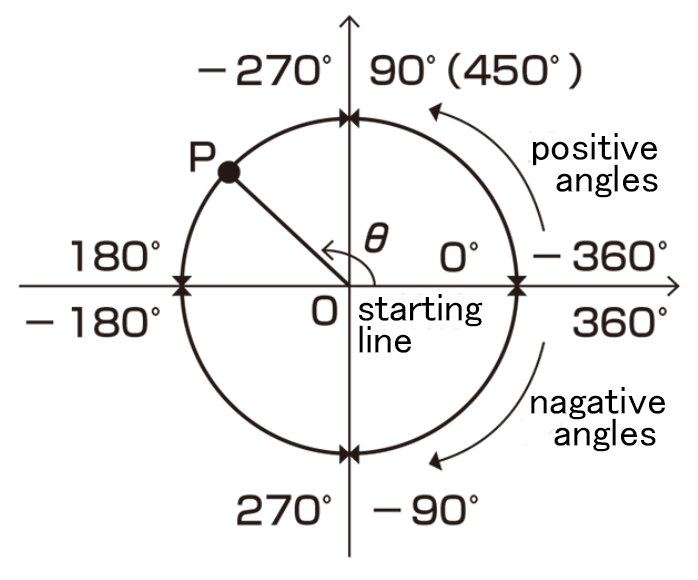
Trigonometric functions also include angles greater than 360° and negative angles.
These cannot be measured with a protractor, so a circle called a unit circle is used as a protractor.
An angle upward from the starting line is called a positive angle, and an angle downward is called a negative angle.
A semicircle is 180°, a quarter circle is 270°, and a full circle is 360°. 90° further on, you get 450°.
The same is true for negative angles, but the direction of rotation is reversed. Angles greater than 360°, or negative angles, are called angle magnification.
In the circle shown in the figure, the kinetic radius OP is called the radius vector.
For example, let’s consider a case where the radius vector is at an angle θ. If it is rotated by ±360° and goes around once, it will return to its original position. If it is rotated by another ±360°, it will also return to its original position.
θ±360°, θ±2×360°… are in the same position
Extension of trigonometric ratios (trigonometric functions)
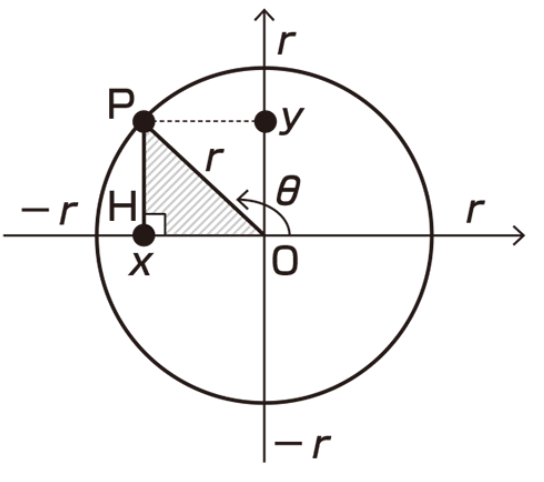
On a circle of radius r centered at the origin O, we take a point (x, y) so that the position of the radius OP is θ. If we then drop a perpendicular line from point P onto the x-axis at the foot of H, we create a right-angled triangle OPH on the circle.
When working with trigonometric ratios, it’s important to keep right-angled triangles in mind.
sinθ, cosθ, and tanθ can be negative values depending on the values of the x and y coordinates.
This is called an extension of trigonometric ratios or trigonometric functions. From the diagram above, we can derive the following rules: